1078. Степень строки

Обозначим через a * b конкатенацию строк a и b. Например, если a = “abc” и b = “def”, то a * b = “abcdef”. Если считать конкатенацию строк умножением, то можно определить операцию возведения в степень следующим образом:

a⁰ = “” (пустая строка)

aⁿ⁺¹ = a * aⁿ

По заданной строке s необходимо найти наибольшее значение n, для которого s = aⁿ для некоторой строки a.

Вход. Каждый тест состоит из одной строки s, содержащей печатные (отображаемые) символы. Строка s содержит не менее одного и не более миллиона символов.

Выход. Для каждой входной строки s вывести в отдельной строке наибольшее значение n, для которого s = aⁿ для некоторой строки a.

Пример входа	Пример выхода
abcd aaaa ababab	1 4 3

РЕШЕНИЕ

строки – префикс-функция

Анализ алгоритма

Рассмотрим слово S длиной len, являющееся повторением слова A n раз. То есть S = Aⁿ. Пусть длина слова A равна k, причем оно само не является повторением никакого слова.

Построим префикс-функцию p слова S. Поскольку индексы строки начинаются с нуля, то подстрока S[k ...2k – 1] является копией S[0 ...k – 1] и соответственно p[k] = 1, p[k + 1] = 2, …, p[2k – 1] = k. Третий повтор слова A находится в позициях S[2k ...3k – 1] и при этом p[2k] = k + 1, p[2k + 1] = k + 2, …, p[3k – 1] = 2k. Последняя ячейка префикс - функции p[nk – 1] равна (n – 1)k.

Вычислим разницу: len – p[len – 1] = nk – (n – 1)k = k, что равно длине слова A. Тогда степень n слова S равна len / k. При этом если len не делится на k, то S не является повторением никакого слова и следует положить n = 1.

Пример

Рассмотрим строку S = (abc)⁴. Построим ее префикс-функцию:

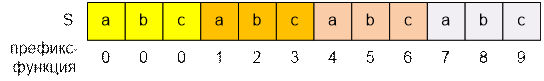
Количество повторов слова abc в S равно n = 4, а длина повторяющегося слова равна k = 3. Последняя ячейка префикс - функции p[nk – 1] = p[11] равна (n – 1)k = 9. Разница len – p[len – 1] равна 12 – 9 = 3, что равно длине слова abc.

Реализация алгоритма

В векторе p строим префикс-функцию строки s.

vector<int> p;

string s;

Функция MaxBorderArray строит и возвращает префикс-функцию строки s.

vector<int> MaxBorderArray(string& s)

{

vector<int> p(s.size(), 0);

p[0] = 0;

for (int i = 1; i < s.size(); i++)

{

int j = p[i - 1];

while ((j > 0) && (s[i] != s[j])) j = p[j - 1];

if (s[i] == s[j]) p[i] = j + 1; else p[i] = 0;

}

return p;

}

Основная часть программы. Читаем входную строку s, вычисляем ее длину len. Вычисляем в массиве p префикс-функцию.

while (cin >> s)

{

len = s.size();

p = MaxBorderArray(s);

Вычисляем разницу между длиной слова и длиной самого длинного префикса строки s, совпадающей с ее суффиксом.

k = len - p[len-1];

Если длина слова len не делится на полученную разницу k, то входная строка s не является степенью никакой строки. Иначе степень строки s равна len / k.

if (len % k) n = 1; else n = len / k;

cout << n << endl;

}